S'évaluer

Sphère d'influence

Difficulté : ☆☆ Temps : 30 min

La sphère d'influence d'une planète de masse 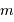orbitant sur une orbite circulaire de rayon 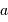autour de son étoile de masse 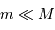$m\ll M$ peut-être définie comme la zone à l'intérieur de laquelle un satellite reste piégé autour de la planète (à l'extérieur de cette sphère, le satellite est capturé en orbite autour de l'étoile). Pour déterminer le rayon de cette sphère, on cherche dans le référentiel tournant avec la planète la position d'équilibre entre les 2 corps 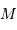et . 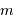On note 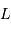cette position (1er point de Lagrange).

Question 1)

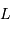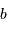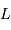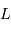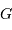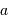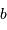La distance de à la planète étant notée , déterminer les distances de à l'étoile et de au barycentre du système (planète-étoile) en fonction de et . On note 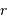cette dernière distance.

Aide [2 points]

Question 2)

Montrer, en identifiant les différents termes, que la relation suivante définit l'état d'équilibre du satellite dans le référentiel barycentrique :

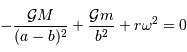
$-{{\cal G}M\over (a-b)^{2}}+{{\cal G}m\over b^{2}}+r\omega^{2}=0$

Aide Aide [3 points]

Question 3)

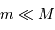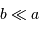Développer cette relation en ne retenant que les termes d'ordre 0 ou 1 ( $m\ll M$ et $b\ll a$ ). En déduire que :

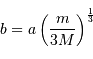
$b=a\left({m\over 3M}\right)^{1\over 3}$

Aide [3 points]

Question 4)

Application numérique :

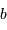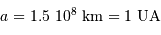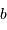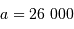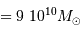Calculer pour la Terre ( $a = 1.5\ 10^{8}\ \mathrm{km} = 1\ \mathrm{UA}$ ) et comparer à la distance Terre-Lune (380 000 km). 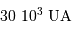Calculer pour le Soleil qui orbite autour du centre galactique ( $a = 26\ 000$ années de lumière, masse $= 9\ 10^{10} M _{\mathrm{\odot}}$ ), et comparer à la distance moyenne entre deux étoiles (distance Soleil-Proxima du Centaure = 4.2 AL), ainsi qu'à la distance du nuage de Oort (de l'ordre de $30\ 10^{3}\ \hbox{UA}$ ).

Aide [2 points]