
|
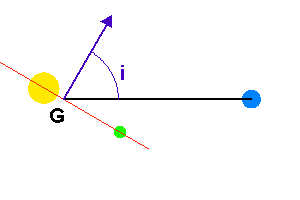
 est défini entre la normale au plan de la trajectoire (vu par la tranche, trace rouge) et l'axe de visée.
est défini entre la normale au plan de la trajectoire (vu par la tranche, trace rouge) et l'axe de visée.
Pour toute la suite :
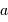 .
.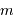 la masse de la planète, et
la masse de la planète, et 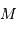 celle de l'étoile.
celle de l'étoile.
On suppose que, d'après les modèles stellaires, la mesure du spectre de l'étoile permet d'estimer sa masse 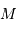 . Mais une variable reste inconnue : l'inclinaison
. Mais une variable reste inconnue : l'inclinaison  sous laquelle on voit le système orbital.
Les principales caractéristiques de l'orbite de la planète peuvent être déduites de la mesure de décalage Doppler.
sous laquelle on voit le système orbital.
Les principales caractéristiques de l'orbite de la planète peuvent être déduites de la mesure de décalage Doppler.
L'analyse du spectre de l'étoile modulé par effet Doppler fournit le graphe de la vitesse radiale de l'étoile en fonction du temps, 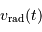 .
Ce type d'observation spectrométrique fournit deux observables :
.
Ce type d'observation spectrométrique fournit deux observables :
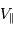 , parallèle à l'axe de visée (car l'effet Doppler est sensible à la seule composante
, parallèle à l'axe de visée (car l'effet Doppler est sensible à la seule composante 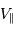 ).
).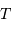 de rotation du système.
de rotation du système.
Ces observables sont des caractéristiques liées à l'orbite du système. On ne sait toujours rien sur la planète elle-même. La 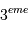 loi de Kepler appliquée au couple planète-étoile relie le rayon de l'orbite à la période de rotation :
loi de Kepler appliquée au couple planète-étoile relie le rayon de l'orbite à la période de rotation :
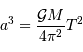
En utilisant la loi de conservation de la quantité de mouvement (le système est isolé), on peut accéder à la masse de la planète :
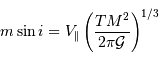
où 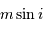 est la masse de la planète
est la masse de la planète 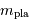 affectée du facteur
géométrique
affectée du facteur
géométrique 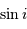 , inconnu.
Le calcul complet est proposé en exercice.
, inconnu.
Le calcul complet est proposé en exercice.
Statistiquement, la probabilité d'avoir une inclinaison  dépend de l'ouverture du cône de demi-angle au sommet
dépend de l'ouverture du cône de demi-angle au sommet  : elle vaut
: elle vaut 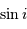 .
La probabilité de voir un système de face (i=0) est bien moindre que celle de le voir par la tranche (i=π/2). En effet, il y a une seule direction qui pointe de l'étoile vers la Terre, donc confondue avec l'axe de visée, mais une infinité qui lui sont perpendiculaires.
.
La probabilité de voir un système de face (i=0) est bien moindre que celle de le voir par la tranche (i=π/2). En effet, il y a une seule direction qui pointe de l'étoile vers la Terre, donc confondue avec l'axe de visée, mais une infinité qui lui sont perpendiculaires.
En moyenne, le paramètre 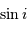 vaut
vaut 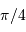 ;
ce calcul est proposé en exercice.
;
ce calcul est proposé en exercice.