
|
Difficulté : ☆☆☆ Temps : 45 min
Cet exercice se propose de montrer que la précision astrométrique
d'un satellite tel Hipparcos ou Gaia peut être estimée par
l'application des inégalités de Heisenberg. On s'intéresse pour
ceci à la propagation d'un photon, issu d'un objet ponctuel à
l'infini, dont la trajectoire intercepte le miroir primaire de
détection (!). On munit l'espace d'un repère orthonormé 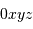 telle que le plan
telle que le plan 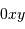 corresponde au miroir primaire de la
détection. La quantité de mouvement du photon incident est
quasiment parallèle à
corresponde au miroir primaire de la
détection. La quantité de mouvement du photon incident est
quasiment parallèle à 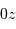 . On suppose que la formation d'image
suit parfaitement les lois de l'optique géométrique.
. On suppose que la formation d'image
suit parfaitement les lois de l'optique géométrique.
On s'intéresse à l'interception du photon selon la direction 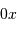 .
Peut-on connaître la position de l'impact et de la réflexion du
photon sur le miroir? En déduire que le front d'onde incident est
découpé en tranche de largeur la dimension du miroir, que la
position selon l'axe
.
Peut-on connaître la position de l'impact et de la réflexion du
photon sur le miroir? En déduire que le front d'onde incident est
découpé en tranche de largeur la dimension du miroir, que la
position selon l'axe 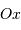 est inconnue, et que donc elle est
affublée d'une incertitude de position
est inconnue, et que donc elle est
affublée d'une incertitude de position 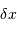 .
.
Aide [2 points]
On rappelle qu'un échantillonnage par valeur entière correspond à
un bruit de numérisation de 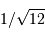 . En déduire
l'incertitude de mesure de la composant selon
. En déduire
l'incertitude de mesure de la composant selon 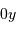 de la quantité
de mouvement du photon.
de la quantité
de mouvement du photon.
Aide [1 points]
Par inégalité de Heisenberg, les incertitudes de position et quantité de mouvement doivent vérifier :
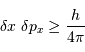
avec la quantité de mouvement totale 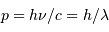 .
En déduire que l'incertitude de repérage de l'angle d'incidence du
photon vaut :
.
En déduire que l'incertitude de repérage de l'angle d'incidence du
photon vaut :
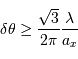
Faire l'application numérique pour Gaia, observant à la longueur
d'onde moyenne de 600 nm, avec 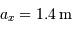 . Cela est-il
compatible avec les performances annoncées, de l'ordre de
. Cela est-il
compatible avec les performances annoncées, de l'ordre de 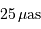 à la magnitude
à la magnitude 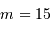 ? Pourquoi ?
? Pourquoi ?
[1 points]
La question précédente dimensionne l'incertitude pour 1 photon. On
montre plus loin dans le cours que pour 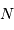 photons effectivement
détectés, l'incertitude est divisée par
photons effectivement
détectés, l'incertitude est divisée par 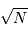 . Combien de
photons doivent être détectés pour aboutir à la performance
annoncée.
. Combien de
photons doivent être détectés pour aboutir à la performance
annoncée.
[1 points]