 Objectifs
Objectifs
Montrer comment les paramètres d'un interférogramme doivent être choisis pour une optimisation de son acquisition respectant la résolution spectrale désirée.
Les paramètres du spectre
Le but de l'interférométrie consiste à obtenir une information spectrale avec les éléments désirés. Les paramètre de l'interférogramme doivent donc obéir à cette contrainte.
Le spectre est essentiellement caractérisé par :
- L'intervalle spectral
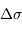 : il correspond au filtre d'entrée, à choisir en pratique parmi un lot de filtres proposés.
: il correspond au filtre d'entrée, à choisir en pratique parmi un lot de filtres proposés. - La résolution spectrale
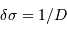 : à ajuster par l'une des propriétés de l'interférogramme.
: à ajuster par l'une des propriétés de l'interférogramme.
Les paramètres de l'interférogramme
Deux paramètres construisent l'interférogramme :
- La différence de marche maximale
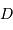
- Le nombre de points
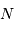 entre la différence de marche nulle
et la différence de marche maximale
entre la différence de marche nulle
et la différence de marche maximale 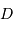 , équidistants de
, équidistants de 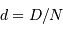 .
.
Le lien entre les paramètres du spectre et de l'interférogramme dérivent des relations suivantes :
- La résolution spectrale est liée à la différence de marche maximale
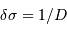
- La largeur de l'intervalle spectral libre est liée au pas de l'interférogramme
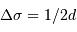
Critère de choix des paramètres de l'interférogramme
Le principe même de la spectrométrie par transformée de Fourier nécessite de sélectionner une région spectrale pas trop large, par un filtre adéquat, autour des raies à étudier. Ceci peut se comprendre de diverses manières : d'un point de vue expérimental, un filtre large va conduire à une teinte plate très rapidement, de laquelle plus aucune information ne sera extractible ; du point de vue de Fourier, il s'agit de pouvoir travailler dans une région limitée du spectre afin qu'un échantillonnage limité, conduisant à un intervalle spectral libre limité, suffise à recouvrer toute l'information spectrale.
Intervalle spectral libre
On note 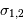 respectivement les bornes inférieure et supérieure de la bande passante utile.
La largeur de la bande passante
respectivement les bornes inférieure et supérieure de la bande passante utile.
La largeur de la bande passante 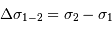 détermine le domaine des nombres d'onde dans lequel il ne doit pas y
avoir confusion spectrale.
détermine le domaine des nombres d'onde dans lequel il ne doit pas y
avoir confusion spectrale.
En d'autres termes, l'échantillonnage doit assurer une fréquence de
coupure spatiale 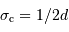 telle que la largeur spectrale
telle que la largeur spectrale ![[\sigma_1, \ \sigma_2]](../pages_fourier/equations_fts-enregistrement/equation12.png) du filtre soit comprise dans l'intervalle spectral libre
du filtre soit comprise dans l'intervalle spectral libre ![[n \sigma _{\mathrm{c}}, \ (n+1) \sigma _{\mathrm{c}}]](../pages_fourier/equations_fts-enregistrement/equation13.png) :
:
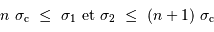
avec 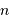 un entier naturel.
un entier naturel.
Choix en pratique des paramètres de l'interférogramme
Il apparaît immédiatement la condition :
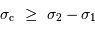 .
Si l'on suppose la différence de marche maximale
.
Si l'on suppose la différence de marche maximale 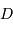 fixée, et donc la
résolution fixée, on peut
préciser le choix du nombre de points optimal
fixée, et donc la
résolution fixée, on peut
préciser le choix du nombre de points optimal 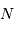 , résultant des 2
conditions ci-dessus.
, résultant des 2
conditions ci-dessus.
En omettant tout d'abord que 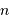 et
et 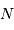 doivent être entiers, leurs solutions réelles doivent vérifier :
doivent être entiers, leurs solutions réelles doivent vérifier :
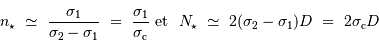
Comme ces 2 solutions ne sont pas nécessairement entières, il s'agit de
déterminer les entiers 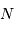 et
et 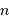 assurant de façon optimale :
assurant de façon optimale :
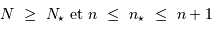
C'est à dire :
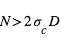 et simultanément
et simultanément
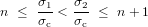
Les 2 inégalités concernant les entiers successifs 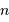 et
et 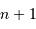 assurent la validité de l'intervalle spectral
assurent la validité de l'intervalle spectral 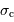 défini par
défini par 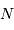 .
.
| paramètres | symbole | unité | |
|---|---|---|---|
| borne min. | 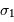
| 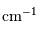 | |
| borne max. | 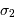
| 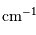 | |
| largeur du filtre | 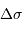 | 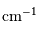 | 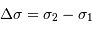 |
| ddm maximale | 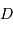 | cm | |
| pas en ddm | 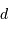 | cm | |
| nombre de ddm | 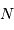 | 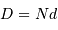 | |
| résolution | 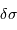 | 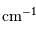 | 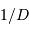 |
| largeur interv. spectr. libre | 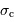 | 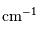 | 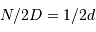 |

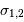 = bornes min et max du filtre)
= bornes min et max du filtre)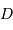 = ddm
maximale)
= ddm
maximale)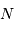 = nbre de points dans l'interférogramme)
= nbre de points dans l'interférogramme)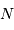 adaptée à l'intervalle spectral
adaptée à l'intervalle spectral
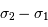 et à la résolution proposée.
et à la résolution proposée.
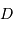 .
.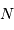 voisin mais différent de la
valeur proposée.
voisin mais différent de la
valeur proposée.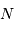 très grand.
très grand.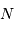 élevées.
élevées.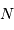 élevées.
élevées.