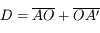SOLUTION

Si on forme l'image de notre objet sur l'écran, alors on a 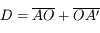$D = \overline{AO} + \overline{OA'}$ .

D'autre part, la relation de conjugaison de Descartes nous dit 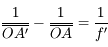$\frac{1}{\overline{OA'}} - \frac{1}{\overline{OA}} = \frac{1}{f'}$

On calcule 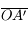$\overline{OA'}$ en fonction de 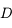et

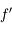
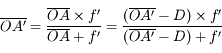
$\overline{OA'} = \frac{\overline{OA} \times f'}{\overline{OA} + f'} = \frac{(\overline{OA'} - D) \times f'}{(\overline{OA'} - D) + f'}$

Après calcul, on obtient :

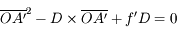
$\overline{OA'}^2 - D\times\overline{OA'} + f'D = 0$

Ah... la bonne vieille équation du second degré ! Calculons-en le discriminant.

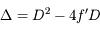
$\Delta = D^2 - 4f'D$

Une solution existe (donc une image sur l'écran), si le discriminant est positif. Il faut donc que 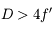D > 4f' . Si la distance entre l'objet et l'écran est inférieure à 4 fois la distance focale, il sera impossible de faire apparaître l'image sur l'écran !