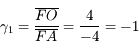 , l'image et l'objet font la même taille mais sont inversés l'un par rapport à l'autre.
, l'image et l'objet font la même taille mais sont inversés l'un par rapport à l'autre.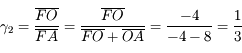 , l'image est 3 fois plus petite et dans le même sens que l'objet.
, l'image est 3 fois plus petite et dans le même sens que l'objet.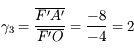 , l'image est 2 fois plus grande et dans le même sens que l'objet.
, l'image est 2 fois plus grande et dans le même sens que l'objet.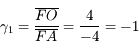 , l'image et l'objet font la même taille mais sont inversés l'un par rapport à l'autre.
, l'image et l'objet font la même taille mais sont inversés l'un par rapport à l'autre.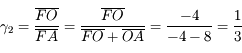 , l'image est 3 fois plus petite et dans le même sens que l'objet.
, l'image est 3 fois plus petite et dans le même sens que l'objet.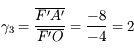 , l'image est 2 fois plus grande et dans le même sens que l'objet.
, l'image est 2 fois plus grande et dans le même sens que l'objet.