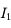 , on a la relation
, on a la relation 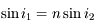 .
.
Nous allons y aller pas à pas. Tout d'abord, au point 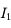 , on a la relation
, on a la relation 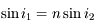 .
.
Au point 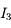 ,
, 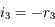 . Exprimons
. Exprimons 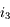 . Dans le triangle
. Dans le triangle 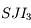 ,
, 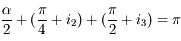 , d'où
, d'où 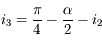
Au point 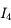 ,
, 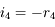 . Exprimons
. Exprimons 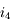 . Dans le triangle
. Dans le triangle 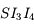 ,
, 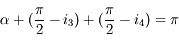 . Donc
. Donc 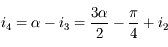 .
.
Enfin, au point 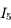 ,
, 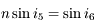 . Exprimons
. Exprimons 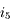 . Dans le triangle
. Dans le triangle 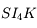 ,
, 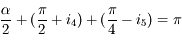 , d'où
, d'où 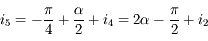
Pour garantir une déviation de 90°, il faut que 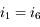 donc
donc 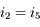 . Cela entraîne que
. Cela entraîne que 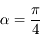
L'angle 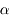 doit donc mesurer 45°
doit donc mesurer 45°