Sans atmosphère : Page pour l'impression

Nous allons à présent aborder les lois quantitatives permettant de modéliser simplement les profils verticaux de température au sein des atmosphères planétaires. Cela nécessite quelques rappels sur le rayonnement thermique, dit de "corps noir".

Spectre du corps noir

L'intensité lumineuse 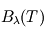$B_{\lambda}(T)$ , définie comme la puissance émise par unité de surface émettrice, par angle solide autour de la direction du rayon et par unité de longueur d'onde 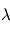$\lambda$ émise par tout corps noir idéal de température 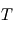, est donnée par la loi de Planck :

$B_{\lambda}(T) = \frac{2 h c^2}{\lambda ^5} \frac{1}{\exp \left( \frac{hc}{\lambda kT} \right) -1}$

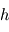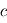où , et 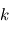désignent respectivement les constantes fondamentales de Planck, de la vitesse de la lumière et de Maxwell-Boltzmann. Cette fonction possède des propriétés mathématiques aux conséquences importantes pour la suite du cours.

Loi de Wien

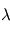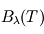Elle donne la position du maximum en $\lambda$ de $B_{\lambda}(T)$ à température 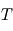donnée, comme illustré précédemment.

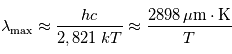
$\lambda_{\mathrm{max}} \approx \frac{hc}{2,821\;k T} \approx \frac{2898\,\mathrm{\mu m \cdot K}}{T }$

Autrement dit, plus le corps est chaud, et plus il émet principalement à des longueurs d'ondes courtes et ce de façon inversement proportionnelle. Cela justifie la séparation du spectre lumineux en :

lumière UV-visible-proche IR : émise par les objets d'une température de quelques milliers de Kelvins. Ainsi, pour le Soleil, 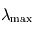$\lambda_{\mathrm{max}}$ est voisin de 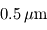$0.5\,\mu\mathrm{m}$ (soit dans le vert).
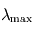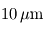infrarouge thermique : émis par les objets d'une température de quelques dizaines à quelques centaines de Kelvins, comme les planètes du système solaire. Ainsi, pour la Terre, $\lambda_{\mathrm{max}}$ est voisin de $10\,\mu\mathrm{m}$ .

La séparation entre les deux domaines est prise de façon conventionnelle autour de 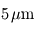$5\,\mu\mathrm{m}$ . Dans le contexte exoplanétaire, une remarque importante s'impose dès maintenant : la plupart des exoplanètes actuellement connues sont extrêmement chaudes, avec des températures excédant souvent 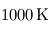$1000\,\mathrm{K}$ , si bien que la limite entre infrarouge thermique et lumière stellaire est décalée vers de plus courtes longueurs d'onde, voire devient complètement dénuée de sens. Cela empêche notamment d'appliquer tels quels les modèles atmosphériques conçus dans le système solaire qui distinguent ces deux catégories.

Loi de Stefan

Lorsque l'on ne s'intéresse pas au détail du spectre émis par le corps noir, il est souvent intéressant de calculer le flux (c'est à dire la puissance par unité de surface émettrice) total émis par le corps noir dans un demi-espace (par exemple, pour une surface planétaire, vers le haut). Pour cela, il suffit d'intégrer la loi de Planck sur sa variable spectrale 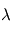$\lambda$ , et sur les 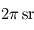$2\pi\,\mathrm{sr}$ d'angle solide en question. Le calcul donne alors le résultat suivant, connu sous le nom de loi de Stefan-Boltzmann :

$F = \sigma T^4$

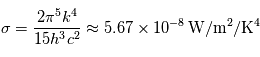où $\sigma = \frac{2\pi^5 k^4}{15h^3c^2} \approx 5.67 \times 10^{-8}\,\mathrm{W/m^2/K^4}$ est connu sous le nom de constante de Stefan-Boltzmann. La puissance émise par un corps noir dépend donc énormément de sa température (une augmentation relative de 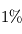$1\%$ de sa température entraîne ainsi une augmentation d'environ 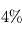$4\%$ du flux émis).

Loi de Kirchhoff

Émissivité

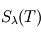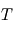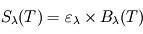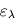Le corps noir est un modèle abstrait que l'on ne rencontre pas dans la vie courante. Le spectre thermique $S_{\lambda}(T)$ émis par un corps donné se trouvant à l'équilibre thermodynamique à la température peut alors s'exprimer comme $S_{\lambda}(T) = \varepsilon_{\lambda}\times B_{\lambda}(T)$ où $\varepsilon_{\lambda}$ est une grandeur sans dimension appelée émissivité (qui dépend de la température, mais de façon moins marquée que la fonction de Planck 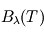$B_{\lambda}(T)$ si bien que par souci d'alléger les notations, on ne la note pas en général 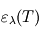$\varepsilon_{\lambda}(T)$ comme on le devrait en toute rigueur).

Loi de Kirchhoff

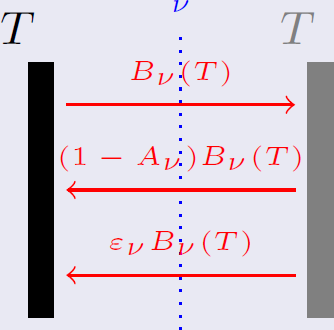
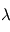Considérons un corps noir en contact radiatif avec un corps réel à travers un filtre laissant seulement passer les radiations à la longueur d'onde $\lambda$ . On sait qu'une fois l'équilibre thermodynamique atteint, ces deux corps en contact radiatif auront la même température 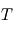. Si l'on note 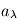$a_{\lambda}$ la fraction du rayonnement incident absorbée par le corps réel, que l'on appelle absorbance, il en renvoie la fraction complémentaire 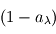$\left( 1 - a_{\lambda} \right)$ . Un bilan net des flux (nul à l'équilibre) à travers le filtre donne alors la relation 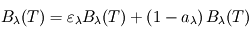$B_{\lambda}(T) = \varepsilon_{\lambda} B_{\lambda}(T) + \left(1 - a_{\lambda} \right) B_{\lambda} (T)$ , ce qui se simplifie en 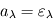$a_{\lambda} = \varepsilon_{\lambda}$ . C'est la loi de Kirchhoff, que L'on résume souvent en "les bons absorbeurs sont les bons émetteurs".

Illustration de la loi de Kirchhoff

Crédit : EM

Conséquences

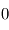Comme l'absorbance est comprise entre et quelle que soit la longueur d'onde, l'émissivité l'est aussi. Il en résulte qu'aucun corps ne peut rayonner plus efficacement que le corps noir à longueur d'onde et température donnée.
Le corps noir ayant par définition une émissivité constante avec la longueur d'onde et égale à , son absorbance est aussi égale à l'unité quelle que soit la longueur d'onde, ce qui justifie son nom de corps noir au sens où il ne réfléchit aucun rayonnement incident.
À l'inverse, un réflecteur parfait qui n'absorberait aucun rayonnement serait également dans l'impossibilité d'émettre quelque rayonnement thermique que ce soit. Une application dans la vie courante de ce phénomène est l'aspect métallique et réfléchissant des objets traités pour éviter les pertes thermiques radiatives : couvertures de survie, bouteilles Thermos : en augmentant leur réflectivité, on abaisse leur absorbance, et donc leur émissivité aussi.

Température d'équilibre sans atmosphère

Cette page développe de façon quantitative les notions vues de façon qualitative ici.

Détermination du flux incident sur la planète

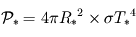
Puissance lumineuse émise par l'étoile : elle s'obtient au moyen de la loi de Stefan-Boltzmann, de la température et de la superficie de la photosphère de l'étoile (sa "surface" visible) : $\mathcal{P}_{*} = 4 \pi {R_*}^2 \times \sigma {T_*}^4$
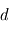Flux reçu au niveau de l'orbite de la planète : en supposant le milieu interplanétaire transparent, la puissance émise par l'étoile se dilue (mais sans absorption) sur des sphères concentriques à l'étoile de plus en plus grandes. En notant la distance de l'étoile à la planète, on obtient alors un flux (puissance par unité de surface réceptrice)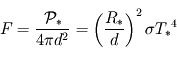 $F = \frac{\mathcal{P}_*}{4 \pi d^2} = \left( \frac{R_*}{d} \right)^2 \sigma {T_*}^4$

Bilan de puissance

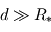Puissance reçue par la planète : l'étoile étant en général assez éloignée de la planète ( $d \gg R_*$ ), les rayons qu'elle émet peuvent être considérés comme parallèles. La façon la plus simple de calculer cette puissance reçue consiste donc à multiplier le flux 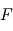par la surface interceptant toute la lumière reçue par la planète à angle droit des rayons. Cette surface consiste donc ici en un disque du rayon 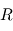de la planète, d'où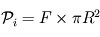 $\mathcal{P}_i = F \times \pi R^2$
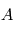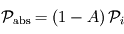Puissances réfléchies et absorbées par la planète : en vertu de la définition de l'albédo bolométrique , la proportion réfléchie de la puissance incidente, la partie absorbée représente donc le complémentaire, soit $\mathcal{P}_{\mathrm{abs}} = \left( 1 - A \right) \mathcal{P}_i$ .
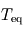Puissance rayonnée thermiquement par la planète : en supposant que la surface de la planète à une température uniforme $T_{\mathrm{eq}}$ se comporte comme un corps noir aux longueurs d'ondes considérées, cette puissance rayonnée vaut alors 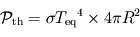$\mathcal{P}_{\mathrm{th}} = \sigma {T_{\mathrm{eq}}}^4 \times 4 \pi R^2$ puisque l'ensemble de la planète rayonne.

Expression de la température d'équilibre

Le bilan radiatif à l'équilibre imposant l'égalité entre la puissance rayonnée par la planète et la puissance absorbée par la planète, on obtient alors l'équation suivante :

$\pi R^2 \left(1 - A \right) F = 4 \pi R^2 \sigma {T_{\mathrm{eq}}^4$

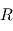qui se résout directement, après simplification du rayon de la planète (ce qui signifie qu'en première approximation, la température d'une planète ne dépend pas de sa taille) en :

$T_{\mathrm{eq}} = \left[ \frac{\left(1 - A\right) F}{4 \sigma} \right]^{1/4} = \sqrt{\frac{R_*}{d}} \left( \frac{1-A}{4} \right)^{1/4} T_*$

ce qui permet de constater que cette température décroît avec la distance à l'étoile, et est proportionnelle à celle de l'étoile. Ainsi, toutes choses égales par ailleurs, pour une étoile naine rouge d'une température moitié de celle du Soleil, il faut pour conserver une température d'équilibre donnée se rapprocher de l'étoile d'un facteur quatre : on peut d'ores et déjà affirmer que les zones habitables autour des petites étoiles de faible température (naines rouges) sont très proches de ces dernières. 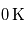Notons au passage que la température d'équilibre d'une planète est bornée par celle de son étoile, plus précisément comprise entre $0\,\mathrm{K}$ (à très grande distance) et 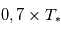$0,7 \times T_*$ à la limite où l'orbite de la planète est tangente à son étoile (et la planète de rayon négligeable devant l'étoile).

Sans atmosphère

Lois du corps noir

Spectre du corps noir

Loi de Wien

Loi de Stefan

Loi de Kirchhoff

Émissivité

Loi de Kirchhoff

Conséquences

Température d'équilibre sans atmosphère

Détermination du flux incident sur la planète

Bilan de puissance

Expression de la température d'équilibre