
|
Etablir le bilan de la puissance rayonnée par un corps noir stellaire.
Quelle puissance rayonne une étoile de température d'équilibre 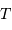 , assimilable à un corps
noir de température
, assimilable à un corps
noir de température 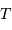 , supposée sphérique de rayon
, supposée sphérique de rayon 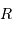 ? La réponse
nécessite d'intégrer la luminance spectrale du corps noir sur toute sa
surface, dans toutes les directions, à toute longueur d'onde.
? La réponse
nécessite d'intégrer la luminance spectrale du corps noir sur toute sa
surface, dans toutes les directions, à toute longueur d'onde.
Le calcul aboutit à la puissance :
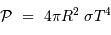
avec la constante de Stefan : 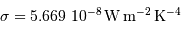 .
.
On peut justifier rapidement la présence des termes 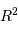 et
et 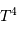 dans cette puissance totale rayonnée.
En effet, l'intégration de la luminance spectrale, spatiale, angulaire et spectrale :
dans cette puissance totale rayonnée.
En effet, l'intégration de la luminance spectrale, spatiale, angulaire et spectrale :
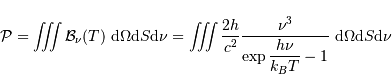
implique, pour la dépendance en fonction du rayon, un terme proportionnel à la surface
stellaire, variant donc comme 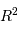 , et pour le terme de température, un
terme proportionnel à
, et pour le terme de température, un
terme proportionnel à 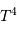 , mis en évidence par le changement de
variable
, mis en évidence par le changement de
variable 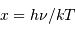 , qui conduit à :
, qui conduit à :
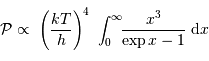
Les termes non explicités dans cette équation ne dépendent pas de la
température, pas plus que l'intégrale sur la variable 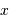 , qui n'est
plus qu'un simple nombre
, qui n'est
plus qu'un simple nombre 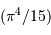 .
.
La loi en 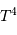 entraîne une grande diversité dans la vie des étoiles.
Deux étoiles de rayons analogues mais avec des températures variant du simple au
quintuple (4000 - 20000 K p.ex.) vont avoir des luminosités dans un rapport de
625, donc déjà des couleurs et luminosités très différents. Mais il s'ensuit
également des conséquences très fortes sur leurévolution.
entraîne une grande diversité dans la vie des étoiles.
Deux étoiles de rayons analogues mais avec des températures variant du simple au
quintuple (4000 - 20000 K p.ex.) vont avoir des luminosités dans un rapport de
625, donc déjà des couleurs et luminosités très différents. Mais il s'ensuit
également des conséquences très fortes sur leurévolution.