
|
Reconstituer les éléments géométriques de l'orbite vraie du système.
Eléments géométriques définissant une trajectoire elliptique.
L'observation donne une série de positions relatives des deux étoiles sur le ciel. En choisissant l'étoile la plus brillante (E2) comme origine des coordonnées, les positions de l'étoile la plus faible (E1) s'agencent sur une ellipse, mais il apparaît que E2 n'est pas au foyer de l'orbite projetée.
Soit O le centre de l'ellipse apparente et A à l'intersection de la droite OE2 avec l'ellipse, au plus proche de E2 ; O est la projection du centre de l'orbite vraie et A est la projection de son périgée. Le segment [OA] est alors la projection du demi-grand axe de l'orbite vraie.
L'excentricité 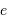 n'est pas plus conservée par la projection que le demi-grand axe, mais la détermination de l'excentricité de l'orbite réelle découle directement des paramètres de l'orbite projetée. Cette excentricité est en effet définie par la distance du foyer (E2) au centre (O), rapportée au demi-grand axe (0A). Ce rapport se mesure directement par OE2/OA, qui est conservé par la projection (par application du théorème de Thalès).
n'est pas plus conservée par la projection que le demi-grand axe, mais la détermination de l'excentricité de l'orbite réelle découle directement des paramètres de l'orbite projetée. Cette excentricité est en effet définie par la distance du foyer (E2) au centre (O), rapportée au demi-grand axe (0A). Ce rapport se mesure directement par OE2/OA, qui est conservé par la projection (par application du théorème de Thalès).
On retrouve l'inclinaison  de l'orbite vraie avec le plan du
ciel en reconstituant la projection du cercle principal de
l'ellipse vraie : ce cercle se projette suivant une ellipse dont
le rapport d'axes est égal à
de l'orbite vraie avec le plan du
ciel en reconstituant la projection du cercle principal de
l'ellipse vraie : ce cercle se projette suivant une ellipse dont
le rapport d'axes est égal à 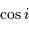 .
.
On utilise pour cela une propriété de l'ellipse et de son cercle
principal : la direction parallèle au diamètre conjugué du grand
axe passant par un point 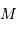 de l'ellipse coupe le cercle
principal en un point
de l'ellipse coupe le cercle
principal en un point 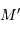 et le grand axe en un point
et le grand axe en un point 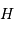 , tels
que
, tels
que 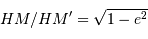 . Cette propriété se conservant par
projection on peut donc reconstituer l'ellipse projection du
cercle principal point par point à partir de la trajectoire
observée et de la direction conjuguée, i.e. la direction de la
tangente à l'ellipse observée aux points
. Cette propriété se conservant par
projection on peut donc reconstituer l'ellipse projection du
cercle principal point par point à partir de la trajectoire
observée et de la direction conjuguée, i.e. la direction de la
tangente à l'ellipse observée aux points 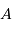 et
et 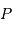 .
.
Le
demi-grand axe de l'orbite vraie est donc finalement égal à
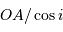 .
.