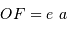|
Présentation des éléments définissant les trajectoires possibles dans le système à 2 corps.
| excentricité | trajectoire | mouvement | énergie mécanique |
|---|---|---|---|
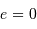 | cercle | lié | minimale et 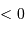 |
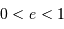 | ellipse | lié | 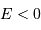 |
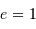 | parabole | libre | 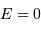 |
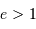 | hyperbole | libre | 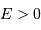 |
Nature de l'orbite selon l'excentricité, dans le cadre du système à 2 corps. La valeur de l'énergie mécanique suppose une référence des énergies potentielles nulle à l'infini.
Les trajectoires qui sont solution du problème à 2 corps dépendent de l'énergie mécanique totale du système et de son moment cinétique, et peuvent être circulaires, elliptiques, paraboliques ou hyperboliques.
En coordonnées polaires, la trajectoire d'un système dans le cadre du problème à 2 corps a pour équation paramétrique :
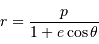
Cette expression peut être obtenue à partir des équations du mouvement du système à 2 corps par l'étude des équations de Binet (voir un cours de physique), ou par le vecteur excentricité.
Deux paramètres suffisent à définir la trajectoire dans son plan.
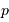 est une longueur reliée au demi-grand axe et à l'excentricité
est une longueur reliée au demi-grand axe et à l'excentricité 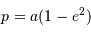 .
.| astre | périastre | apoastre |
|---|---|---|
| Soleil | périhélie | aphélie |
| Terre | périgée | apogée |
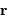 est défini par rapport au foyer
est défini par rapport au foyer 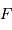 de
l'ellipse définissant le centre de force, et non par rapport au centre
de
l'ellipse définissant le centre de force, et non par rapport au centre 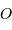 .
.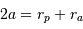 , avec
, avec 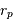 et
et 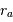 les
rayons des péri- et apoastres
les
rayons des péri- et apoastres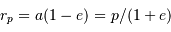
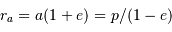
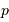 de l'ellipse vérifie
de l'ellipse vérifie 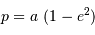
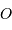 au foyer
au foyer 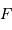 vaut
vaut